자료를 범위로 나눠서 개수를 세고 그것을 비율로 바꿔서 표현할 수 있다. 이것이 히스토그램을 그리는 방법이다. 아래 표를 보자.

대한민국 근로자 가구의 월 소득 분포를 나타낸 표이다. 아래보는 그림은 잘못된 표다. 세로축과 가로축을 보자. 세로축은 비율, 가로축은 소득을 나타낸다. 아마추어가 봐도 이 그림은 잘못됐다. 뭐가 문제 일까? 세로축이 잘못됐다. 세로축을 비율로하니 너무 커진다. 소득이 600만원 이상인 경우는 많이 없기에 모두 묶어줬다. 비율로 높이를 삼으니 블록의 면적이 확 커진다는 걸 알 수 있다.

이번에는 아래 그림을 보자. 이 그림은 잘 나타낸 그림이다.

우선 계급구간별로 비율을 폭으로 나누어 해당 블록의 높이로 삼는다. 블록 면적이 해당 계급구간에 속한 자료의 비율을 나타낸다. 이 그림은 밀도를 세로축으로 썼다. 여기서 밀도는 인구 밀도와 비슷하다. 좁은 지역에 인구가 많으면 인구밀도가 높고 넓은 지역에 사람이 적게 살면 인구밀도는 좁다. 마찬가지다. 600-1000 구간은 범위가 넓다. 거기에 14%가 있다는건 그만큼 밀도가 낮다는 뜻이다. 반대로 좁은 구역(600-1000을 제외한 나머지)에 살면 밀도는 높아진다. 똑같은 구역에 14%가 살아도 밀도는 다를 수 밖에 없다.
히스토그램에서 블록의 높이는 밀도, 즉 가로축의 단위구간에 속한 자료의 비율을 나타낸다. 세로축에 밀도 단위가 사용되는 경우 블록 면적은 해당 구간에 속하는 자료의 비율을 나타내고, 히스토그램 아래 전체 블록의 면적은 100%가 된다.
면적이 비율을 나타내도록 그려진 히스토그램, 그때의 세로축을 밀도단위라고 한다. 세로축이 밀도이기 때문에 가로축에 폭을 곱하면 면적이 확률이된다. 즉 면적은 상대도수가 된다.
히스토그램 예시 : Yellowstone의 Old Faithful
나는 이제껏 봉우리가 하나만 있는 분포만 봤고 그런 분포만 있는 줄 알았다. 착각이었다. 아래 그림은 내가 얼마나 멍청한지 깨닫게 해주는 그림이다. 이런 그림을 쌍봉 분포라고 한다. 쌍본분포는 최빈값을 두개 가지는 분포다.

이 그림은 미국 Yellowstone 국립공원 내 간헐천의 분출 지속기간 분포이다. 분출 지속기간의 히스토그램은 3.2분 기분, 두 개 봉우리를 갖는 쌍본 분포라고 한다.

위 그림은 간헐천이 분출하고 다음 분출까지의 대기시간을 보여주는 그림이다. 이 그림은 70분 기준으로, 두 개 봉우리를 갖는 쌍봉 분포이다. 쌍봉분포라는 사실을 무시하고 단일의 정규분포로 근사하면 잘못된 그림이다.
두 그림을 비교해보자. 뭔가 연관관계가 찾아지지 않나? 그렇다. 간헐천이 물을 많이 뿜으면 대기시간은 길어진다. 물을 많이 뿜었기 때문에 그만큼 지하 물탱크가 물이 차는 시간이 걸린다. 반면 물을 뿜는 시간이 짧으면 대기시간은 짧아진다. 이것을 보기위해 그림을 가지고 우리가 생각하는 것을 표현한다.
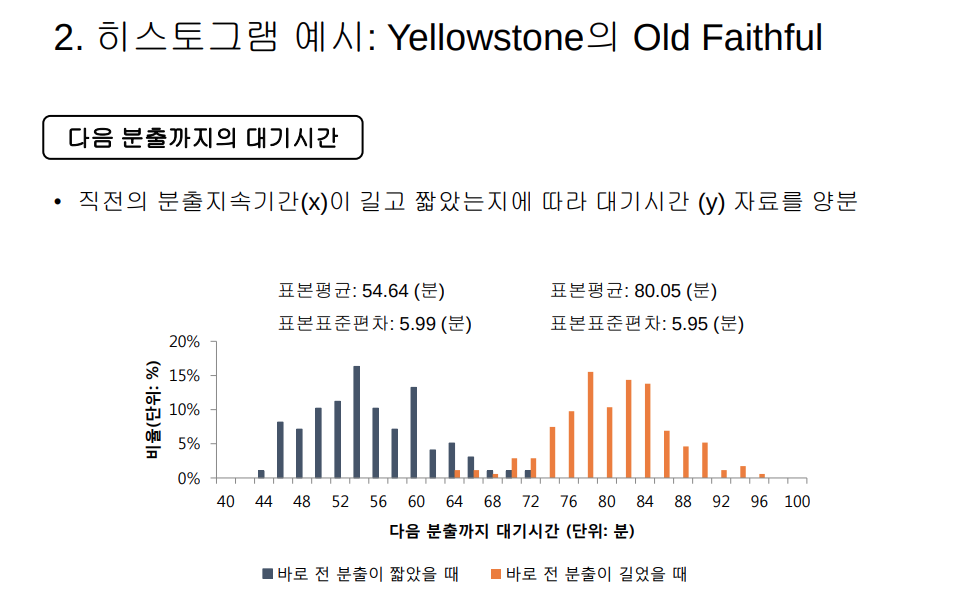
파랑색은 분출 시간이 3분이하 일 때, 빨강은 분출 시간이 길었을 때를 나타낸다. X축은 분출 지속시간을 나타내고 Y축은 다음 분출까지 기다리는 시간을 나타낸다. 앞 두 그림이 관계가 있을 까 해서 따로따로 때어내 그림을 나타냈다. X가 3분 이하인 부분집단만 모아서 히스토그램을 그린 것이 파란색 히스토그램, X가 3분이상인 자료들만 모아서 그 자료들만 가지고 히스토그램을 그린 것이 빨간 히스토그램이다.
'통계학 > 경제통계학 1부 : 그림과 수치를 이용한 자료의 정리' 카테고리의 다른 글
| 표준편차와 자유도 (0) | 2025.04.30 |
|---|---|
| 3 - 3. 혼돈요인 통제 : 따로따로 분석하기 (0) | 2025.04.24 |
| 3 - 1 그림을 이용한 자료정리 (0) | 2025.04.24 |
| 종적 자료의 척도와 정리 (0) | 2025.04.23 |
| 통계란 무엇인가? (1) | 2025.04.23 |



