1. 실제값과 추정치의 차이
제곱근 평균 제곱 오차(root mean square error) RMSE
RMSE란? RMSE는 모델이 예측한 값과 실제 관측값 사이의 차이를 측정하는 방법이다. 쉽게 말해 평균적으로 예측이 실제값으로부터 얼마나 떨어져 있는가를 나타낸다.
RMSE의 특징
단위 : RMSE는 원래 데이터와 같은 단위를 가진다. 예를 들어, 키를 예측하는 모델이라면 RMSE도 cm단위가 된다.
오차 가중치 : RMSE는 제곱을 사용하기 때문에 큰 오차에 더 많은 가중치를 부여한다. 10cm 오차 하나는 10cm 오차 하나는 1cm오차 100개보다 RMSE에 더 큰 영향을 미친다.
자유도 조정
때로는 추정하는 파라미터 수를 고려해 분모를 n 대신 n-p로 사용하기도 한다. 이를 자유도가 조정된 RMSE라고 한다.
조정된 RMSE = √[Σ(y - ŷ)² / (n-p)]
해석 : RMSE 값이 작을수록 모델의 예측 정확도가 높다고 해석한다.
RMSE와 표준편차의 관계
RMSE는 회귀 모델에서 오차의 표준편차와 개념적으로 유사합니다. 회귀선으로부터 데이터 포인트들이 퍼져 있는 정도를 측정하는 값으로, 데이터가 회귀선 주변에 얼마나 집중되어 있는지 보여준다.
RMSE가 작을수록 데이터 포인트들이 회귀선에 가깝게 분포하고 있다는 의미이며, 모델의 설명력이 높다고 볼 수 있다.
표준편차와 RMSE의 비교
1. 단순 평균을 사용하는 경우
- 여기서 모든 y값을 평균(ȳ)을 데이터의 대표값으로 사용한다.
- 이것은 마치 X값과 상관없이 항상 동일한 값(ȳ)을 예측하는 수평선을 기준으로 삼는 것과 같다.
- 각 데이터 포인트가 이 수평선으로 부터 얼마나 떨어져 있는지를 측정한 것이 표준편차
2. 회귀분석을 사용하는 경우(RMSE)
- 여기서 X값을 사용하여 회귀선(ŷ = a + bX)을 찾는다.
- 각 데이터 포인트가 이 회귀선으로부터 얼마나 떨어져 있는지를 측정한 것이 RMSE다.
왜 표준편차 >= RMSE인가?
1. 최소제곱법의 원리
- 회귀선은 "오차의 제곱합"을 최소화하도록 설계됩니다.
- 단순평균을 사용하는 밥법은 회귀분석에서 고려할 수 있는 "특수한 경우"에 불과하다.
- 회귀분석은 이 특수한 경우를 포함해 더 넓은 범위의 가능한 선들 중에서 최적의 선을 찾습니다.
2. 극단적인 예"
- X와 Y가 완변한 선형관계라면 모든 데이터 포인트가 정확히 회귀선 위에 있어 RMSE = 0이 됩니다.
RMSE와 표준편차의 관계: 결정계수(R^2)의 의미
두 오차 측정값의 수학적 관계
강의자가 설명한 핵심 관계식은 다음과 같다.
MSE = σ × √(1-R²)
여기서:
- RMSE는 회귀선으로부터의 오차
- σ는 Y의 표준편차(평균으로부터의 오차)
- R²은 결정계수(상관계수의 제곱)
이 공식은 "회귀분석을 통해 오차가 얼마나 줄어드는가"를 정확히 보여줍니다.
회귀분석의 등분산성 가정과 그 의미
등분산성이란, 회귀선 주변의 데이터 퍼짐이 X값에 상관없이 일정한 상태를 말한다. 회귀선을 따라 어디를 보든 Y값의 분산이 비슷하다.

회귀분석과 정규분포의 결합: 예측과 신뢰구간
강의자가 설명하는 내용은 회귀분석과 정규분포 이론을 결합하여 예측과 신뢰구간을 구성하는 방법에 관한 것입니다. 자세히 설명해 드리겠습니다.
회귀분석에서의 정규분포 적용
회귀분석에서는 다음과 같은 일반화 과정이 이루어집니다:
- 중심의 일반화: 단일 평균값(ȳ)에서 → 회귀함수(regression function)로
- 분산의 일반화: 표준편차(σ)에서 → RMSE(Root Mean Square Error)로
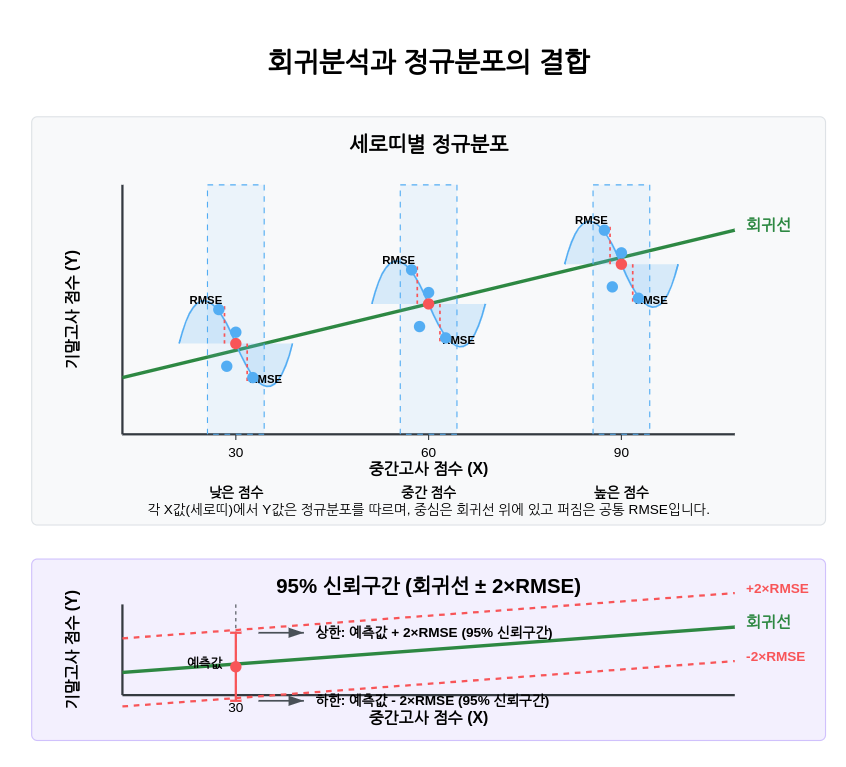
- 분포 가정의 적용: 정규분포를 각 X값(세로띠)에 적용
"세로띠"의 개념
강의자가 말하는 "세로띠"는 특정 X값에서 Y값들의 분포를 의미합니다. 그림에서 볼 수 있듯이:
- 중간고사 점수가 낮은 학생들의 세로띠
- 중간고사 점수가 중간인 학생들의 세로띠
- 중간고사 점수가 높은 학생들의 세로띠
각 세로띠 내에서:
- 중심: 회귀선 위의 점(예측값)
- 퍼짐: RMSE로 측정된 분산
- 분포 형태: 정규분포를 가정
등분산성 가정
"모든 세로띠에서 분산이 동일하다"라는 등분산성 가정을 통해, 모든 X값에 대해 동일한 RMSE 값을 적용합니다. 그래서 그림에서 모든 세로띠의 정규분포 곡선이 같은 폭을 가지고 있습니다.
예측과 신뢰구간
회귀분석과 정규분포를 결합하면 예측과 신뢰구간을 구할 수 있습니다:
점 예측(Point Prediction)
- 특정 X값(예: 중간고사 30점)에 대한 예측 Y값은 회귀선 위의 점입니다.
- 예측값 = β₀ + β₁ × X
구간 예측(Interval Prediction)
- 정규분포의 특성을 활용하여 신뢰구간을 구성합니다:
- 68% 신뢰구간: 회귀선 ± 1×RMSE
- 95% 신뢰구간: 회귀선 ± 2×RMSE
- 99.7% 신뢰구간: 회귀선 ± 3×RMSE
예를 들어, 중간고사에서 30점을 받은 학생의 기말고사 점수 예측:
- 회귀식에 X=30을 대입하여 예측값(점 예측)을 구합니다.
- 95% 신뢰구간을 원한다면 "예측값 ± 2×RMSE"로 계산합니다.
- 이 신뢰구간은 "중간고사 30점을 받은 학생의 기말고사 점수가 95% 확률로 이 범위 안에 있을 것"이라는 의미입니다.
회귀분석 일반화 과정의 의미
강의자가 강조하는 점은 회귀분석이 기존에 배운 통계 개념들의 자연스러운 확장이라는 것입니다:
- 평균 → 회귀함수: 단일 값에서 X에 따라 변하는 함수로 확장
- 표준편차 → RMSE: 평균으로부터의 거리에서 회귀선으로부터의 거리로 확장
- 정규분포 적용: 평균과 표준편차를 사용한 정규분포에서 회귀함수와 RMSE를 사용한 조건부 정규분포로 확장
이러한 일반화 과정을 통해 더 복잡한 현실 세계의 문제(인플레이션 예측, 소득 예측 등)에 적용할 수 있는 강력한 통계적 도구를 얻게 됩니다.
요약
회귀분석에서의 정규분포 적용은:
- 각 X값(세로띠)에서 Y값들이 정규분포를 따른다고 가정
- 분포의 중심은 회귀선 위에 위치
- 분포의 퍼짐은 RMSE로 측정
- 등분산성 가정 하에 모든 X값에서 동일한 RMSE 적용
- 정규분포의 특성을 활용해 신뢰구간 구성
이를 통해 단순한 점 예측을 넘어서, 확률적인 예측 범위를 제공할 수 있게 됩니다. 이것이 회귀분석의 강력한 실용적 가치입니다.
'통계학 > 세상에서 가장 쉬운 통계학 입문' 카테고리의 다른 글
| 21강 t분포로 구간추정 (0) | 2025.03.26 |
|---|---|
| 20강 : t 분포 (0) | 2025.03.25 |
| 19강 모평균이 미지인 정규모집단을 구간추정 (0) | 2025.03.21 |
| 18강. 표본분산의 분포는 카이제곱 분포 (0) | 2025.03.21 |
| 17강 정규모집단의 모분산을 추정 (0) | 2025.03.15 |

