정규분포로 히스토그램을 근사

1. 통계자료의 단위변환과 그 사례
확률변수 x가 평균이 μ 분산이 σ^2인 정규분포를 따른다고 할 때 표준정규분포로 만드려면?
1. 먼저 X에서 평균 μ를 빼준다. (X - μ) 이것을 편차라고 한다.
2. 그 다음 이 편차를 표준편차 σ로 나누어준다.
이렇게 만들어진 새로운 확률변수 Z는 표준정규분포를 따른다. 표준정규 분포는 평균이 0 분산이 1이다.
표준정규분포는 다음과 같은 특징을 같는다.하나, 분포의 전반적인 모습은 단위변환에 의해서 변하지 않는다.둘, 평균을 빼줬기 때문에 새로운 평균은 0이 된다.셋, 표준편차로 나눴기 때문에 새로운 편차는 1이 될 수 밖에 없다.
예시)

예시를 들어보자 50점 만점 과목인 탐구에서 표준 점수가 60이면 상68%에 해당한다. 이 구간에 해당 점수를 받은 학생들이 가장 만다. 표준 점수가 70이면 상당히 잘한 것이다. 여기선 상위 97.5%에 해당한다. 언어 수리 외국어 영역은 탐구에 두배를 해준 값이다. 만약 표준 점수가 120점이면 보통 학생 점수다. 이 구간에 학생들이 가장 많기 때문이다. 140점을 맞으면 매우 뛰어난 학생이다. 여기선 탐구와 마찬가지로 상위 2.5%에 해당한다.

여기서 단위 변화으로 7을 더해주고 3을 곱해줬다. 그러나 모양에 큰 변환은 없다. 위치만 스케일만 바뀔 뿐이다.
2. 정규분포곡선의 특징

확률밀도 함수(Probability Density Function, PDF)는 연속확률변수의 분포를 나타내는 함수다.
확률밀도 함수의 중심은 μ이고 종모양이고 σ만큼 떨어져있다.

사진에 나온대로 표준단위로 -1 부터 1까지 영역의 넓이는 약 68%이고 표준단위로 -2부터 2까지 영역의 넚이는 약 95% 표준단위로 -3부터 3까지 영역의 넓이는 약 99.7퍼센트다. 확률밀도는 확률을 나타내는 밀도이다. 히스토그램으로 있는 밀도와 함수.
여기서 중요한건 중심이 어디인가? μ(평균), 중심으로 부터 관측치 하나하나 확률변수 하나를 뽑을때 중심으로부터 표준적으로 얼마나 떨어지느냐? 분산(σ) 이 두가지로 완변하게 나타낸 함수가 확률밀도함수다.
정리하면 방금전 표준화를 공부했다. 어떤 확률변수 X에서 μ(평균)를 빼주고 표준편차(σ)로 나누면 평균이 0 표준편차가 1인 정규분포를 따르게된다. 이런 정규분포를 함수화 한게 확률밀도함수 되시겠다.

위 사진은 표준졍규분포의 특징을 나타낸다. 평균을 중심으로 좌우 대칭이고, 종 모양이고, 봉우리가 하나이다.
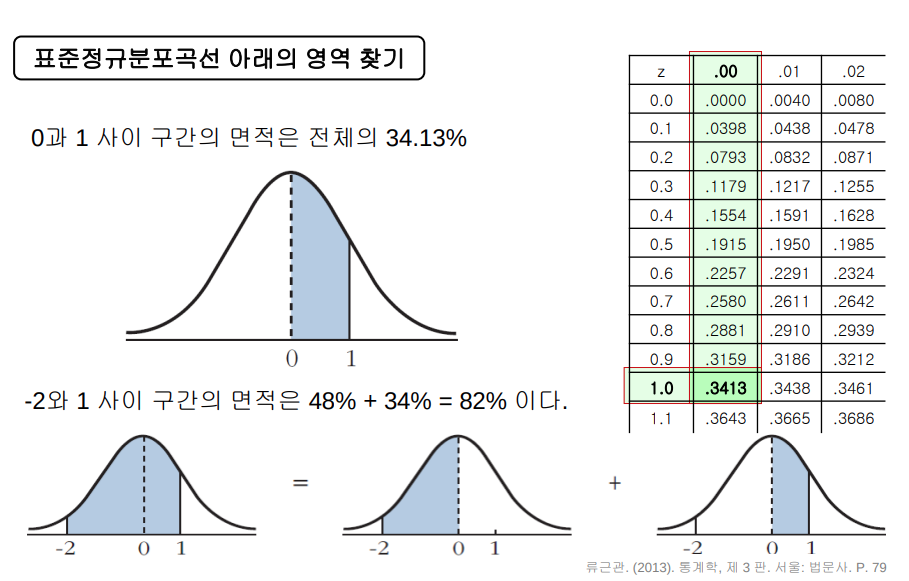
보통 이런건 교과서 맨 뒷장에 있는데 이런 식으로 정규분포 면적을 찾는다.
백분위 수
백분위 수. 영어로 나타내면 Percentile. 숫자 n개를 기준으로 나눈다. 백분위수 가운데 25번째, 50번째, 75번쨰 백분위수를 특별히 1제사분위수, 제2사분위수, 제3사분위수라 부른다. 50번째 백분위수는 제 2 사분위수이면서 중앙값이다.
사분위수 범위를 구하는 방법은
(사분위수 범위) = (제3사분위수) - (제1사분위수)
최소값, 제 1사분쉬수, 제2사분위수, 제3사분위수, 최대값으로 있는 수들을 5Numbersummary 라고 한다.

5 number summary를 그림으로 표현한 거시 boxplot이다.
'통계학 > 경제통계학 1부 : 그림과 수치를 이용한 자료의 정리' 카테고리의 다른 글
| 상관관계와 회귀직선 (0) | 2025.05.05 |
|---|---|
| 상관관계 (0) | 2025.05.01 |
| 표준편차와 자유도 (0) | 2025.04.30 |
| 3 - 3. 혼돈요인 통제 : 따로따로 분석하기 (0) | 2025.04.24 |
| 3 - 2. 히스토그램 그리기 (0) | 2025.04.24 |



