1. 자료의 선형 근사
데이터를 분석하다 보면 변수들간 관계가 비선혀 관계일 수도 있다. 상관계수는 선형관계일 때만 유효하다. 그래서 적절한 조치로 비선형 관계를 선형 관계로 바꿔 줘야한다.

왼쪽 그림은 x와 y가 비선형 관계다. 하지만 y에 로그화 함으로써 x,y는 선형 관계가 됐다. 앞서 공부한 나폴레옹 사례도 보자. 이와 유사한 사례다.

이 자료는 행군하는 거리당 몇명이 죽었는지를 보여주는 함수다. 보시다시피 선형 관계다. 이 자료도 병사수를 나타내는 y를 log화 하면 선형관계를 얻을 수 있다.

선형관계가 된 나폴레옹 군 진격. 여기까지가 워밍업이었다. 이번에는 조금더 자세하고 구체적으로 살펴보자

이 식을

이런 직선을 linear spline equation이라고 한다. 여기서 새로운 개념 knots가 등장한다. knots는 매듭이란 뜻이 있다. 매듭을 어디다 묶어 줄까? 위 식 같은경우는 행군 반환점인 900km지점에 묶었다. knots = 900 (x - 900)+를 수식으로 쓰면 이렇다.
if (x >= 900)
x = x;
else
x - 900 = 0;
x가 0일때 x를 그대로 취한다. 그러니 저 식 12.78 - 0.0012x - 0.0019(x - 900)+에서 900 이전에는 0.0019(x - 900)+이 값을 안쓴다고 보면 된다. x를 10으로 잡으면 10km 당은 계수가 0.012다. 퍼센테이지로 따지면 1.2%. 10km당 1.2명이 죽은 꼴이다. 이제 퇴각할떼 (900km 이후)를 보자. 여기서는 저 식을 그대로 쓰면된다. 퇴각 이전 기울기 0.012에 추가 기울기 0.019를 더하면 0.031. 즉 3.1%가 된다. 퇴각할때는 진군할 때 3배인 3.1명이 죽는 꼴이 된다.
2. 상관관계와 실제 관계
통계공부를 하면서 가장 많이 들은 말은? 상관관계는 인과관계가 아니다! 아래는 이 말의 훌륭한 논거로 삼을만한 그래프이다.
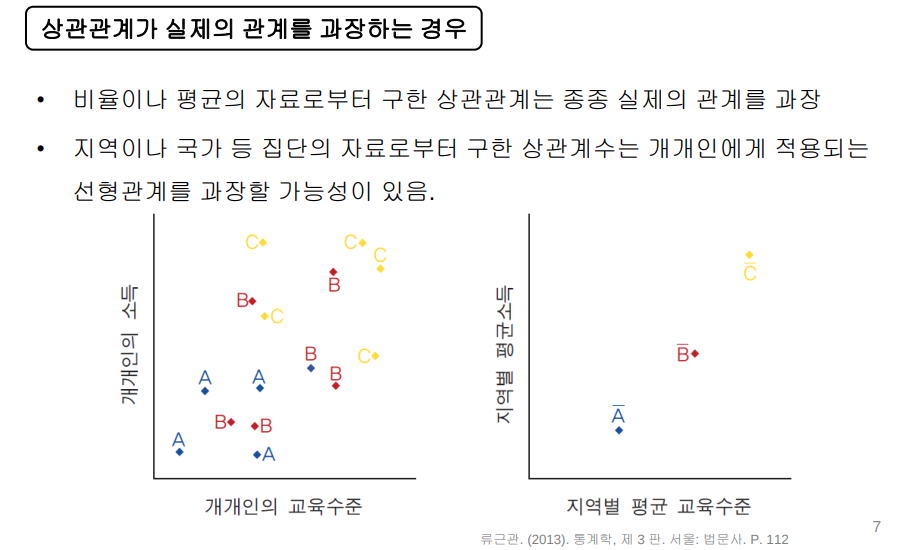
A, B, C는 각각 도시이다. 세로축은 개인 소득, 가로축은 개인의 교육수준이다. 개인 하나하나를 조사해 교육수준과 소득의 상관관계를 알아봤다. 개개인의 소득은 하나씩 찍어 산포도로 나타냈다. 오른쪽 그림을 보자. 오른쪽은 지역별 평균 소득과 지역별 교육 수준의 상관관계를 나타냈다. 결론부터 말하면 이 그림은 잘못됐다. 교육을 받는 건 개인이지 도시가 아니다. 개개인이 교육을 받을 때 개개인의 소득이 어느정도 영향을 받아서 변화하는지를 확인해야 한다. 오른쪽 그림은 잘못된 그림이다.
상관계수가 인과관계는 아니다.

결론: 가짜 상관관계
운동화 가격과 교수 월급 사이에는 높은 상관계수(0.9)가 존재하지만, 실제로 두 변수 사이에 인과관계는 없습니다.
두 변수 모두 시간이라는 제3의 변수에 영향을 받아 증가한 것일 뿐입니다. 이처럼 시계열 데이터에서는 시간적 추세로 인한 가짜 상관관계가 자주 발생합니다.

'통계학 > 경제통계학 1부 : 그림과 수치를 이용한 자료의 정리' 카테고리의 다른 글
| 회귀분석 (0) | 2025.05.06 |
|---|---|
| 일반 선형 회귀모델과 로그 변환 모델의 차이 (0) | 2025.05.05 |
| 상관관계 (0) | 2025.05.01 |
| 정규분포로의 근사 (2) | 2025.05.01 |
| 표준편차와 자유도 (0) | 2025.04.30 |


