1. 정규분포의 성질을 이용해 '예언'을 할 수 있다.
만약 주목하고 있는 불확실한 현상이 정규분포라고 간주한다면, 정규분포의 성질을 이용해서 어떠한 예언을 할 수 있지 않을까요? 이 질문이야 말로 '통계적 추정'의 출발점 입니다.
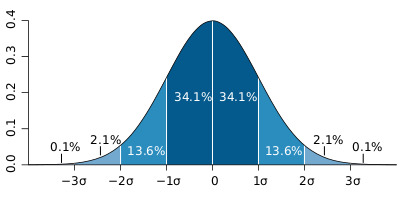
자고로 예측은 '나타날 가능성이 가장 큰 확률'로 해야 현명한 방법입니다. 표준정규분포를 다시 한번 볼까요? x축이 경우의 선택할 숫자 이고, y축이 확률(정확히는 상대도수)이면 0에 가까운 수를 선택하는 것이 가장 똑똑합니다. 왜냐하면 0에 가까울 수록 확률이 올라가기 때문이죠. 하지만 숫자를 하나만 선택해서 예언하는건 극악 무도할 정도로 어려운 일 입니다. 표준정규분포는 어떤 수든지 데이터로 나타날 가능성이 있어 (1/무한대) = 0이기 때문입니다. 그래서 어느 폭을 지정해 'x이상 x이하' 라는 식으로 예언하는 게 현명합니다.
예언하기 가장 좋은 범위는 어디일까요? 범위가 -1에서 1까지인 데이터의 상대도수는 68.2% 입니다. 예언 구간을 -1이상 +1이하의 수로 하면 약 68.26의 확률로 그 예언을 맞출 수 있습니다.
2. 표준정규분포의 95% 예언적중 구간
적중확률을 높이고 싶으면 이 범위를 넓혀야 합니다. 어디까지 넓히는 게 현명할 까요? 보통 많이 사용하는 구간이 '95% 적중' 혹은 '99% 적중' 입니다. 95% 적중 범위를 고른다를 달리 해석하면 5% 예언은 틀린다는 말이 됩니다.
95%확률은 어디서 나온 걸 까요? 저희는 앞 강의에서 '-2이상 +2 이하의 수'의 상대도수는 약 95.44 인것을 말 했습니다. 통계학에서는 적중 확률을 95%로 보기 때문에 구간을 좁혀서 약 '-1.96 이상 1.96이하' 범위를 95% 적중의 에언 구간으로 삼았다. 명심해야 할 것은 통계학 기반의 예언은 100%는 없습니다. 다시 한번 말히지만 저 예언도 5%는 틀릴 수 있다는 것을 전제로 합니다.
상대도수가 95%가 되는 구간은 이 구간 말고도 더 있습니다. 예를 들어 -2.1이상 +1.86d이하도 상대도수가 95%가 됩니다. 그러나 이러면 예언의 적중률이 낮아집니다. '-1.96 이상 1.96이하'의 범위는 3.92이고 -2.1이상 +1.86이하 범위는 3.96입니다. 표중정규분포는 대칭축에 가까울 수록 빈도가 높습니다. 범위가 넓을수록 대칭 축에서 멀어지는데 이는 빈도가 낮으므로 적중율이 낮을 수록 좋습니다.
일반정규분포의 95% 예언적중 구간
평균값이 μ이고 표준편차가 σ인 정규분포의 95% 예언적중 구간은 ( μ - 1.96 σ ) 이상 ( μ + 1.96 σ )이하가 됩니다.
일반정규분포를 표준정규분포로 바꾸는 공식
데이터 x가 평균값이 μ 이고, 표준편차가 σ인 일반정규분포를 따르는 데이터일 때 z=(x - μ) / σ라는 가공을 하면 데이터 z는 표준정규분포를 따르는 데이터가 된다.
일반정규분포의 95% 예언적중구간 : 부등식 표시
데이터 x가 평균값이 μ 이고, 표준편차가 σ이며, 일반정규분포를 따르는 경우 일 때, 95% 예언적중구간은 부등식
-1.96 <= (x - μ) / σ <= +1.96을 풀어서 구한 범위다.
'통계학 > 세상에서 가장 쉬운 통계학 입문' 카테고리의 다른 글
| 11강. 모집단과 통계적 추정 (0) | 2025.03.05 |
|---|---|
| 10강 구간 추정 (0) | 2025.03.03 |
| 07 강의 정규분포 (0) | 2025.02.21 |
| 6강. 표준편차 3 (0) | 2025.02.21 |
| 5강 표준편차2 (0) | 2025.02.21 |
